ECON6037 Experimental Economics

Statistical power

Gerhard Riener

g.riener@soton.ac.uk

February 20, 2024

What is power?

What is power?

• We want to separate signal from noise.

• Power = probability of rejecting null hypothesis, given true effect \(\ne 0\).

• In other words, it is the ability to detect an effect given that it exists.

• Formally: \((1 - \beta)\) (1- Error type) error rate.

• Thus, power \(\in (0, 1)\) .

• Standard thresholds: \(0.8\) or \(0.9\).

Starting point for power analysis

• Power analysis is something we do before we run a study.

  • Helps you figure out the sample you need to detect a given effect size.

  • Or helps you figure out a minimal detectable difference given a set sample size.

  • May help you decide whether to run a study.

• It is hard to learn from an under-powered null finding.

  • Was there an effect, but we were unable to detect it? or was there no effect? We can’t say.

Power

• Say there truly is a treatment effect and you run your experiment many times. How often will you get a statistically significant result?

• Some guesswork to answer this question.

  • How big is your treatment effect?

  • How many units are treated, measured?

  • How much noise is there in the measurement of your outcome?

Approaches to power calculation

• Analytical calculations of power

• Simulation

Power calculation tools

• Interactive

  • EGAP Power Calculator

  • rpsychologist

• R Packages

  • pwr

  • DeclareDesign, see also https://declaredesign.org/

Analytical calculations of power

Analytical calculations of power

• Formula: \[\begin{align*} \text{Power} &= \Phi\left(\frac{|\tau| \sqrt{N}}{2\sigma}- \Phi^{-1}(1- \frac{\alpha}{2})\right) \end{align*}\]

• Components:

  • \(\Phi\): standard normal CDF is monotonically increasing
  • \(\tau\): the effect size
  • \(N\): the sample size
  • \(\sigma\): the standard deviation of the outcome
  • \(\alpha\): the significance level (typically 0.05)

Example: Analytical calculations of power

Optimal Sample Size Calculation

Formula by List et al. (2011)

Actual question for experimental economists: How large should the sample be?

• Applicable for experiments with a dichotomous treatment.

• Outcome is continuous.

• t-test used for differences between treatment and control groups.

Optimal Sample Size: Assumptions

Distribution Assumptions

• Outcomes in treatments are normally distributed: \(Y_{it} |X_i \sim N(\mu_t , \sigma^2_t )\).

• \(\delta\) is the minimum average treatment effect detectable.

• Null hypothesis \(H_0\): \(\mu_0 = \mu_1\).

• Alternative hypothesis \(H_1\): \(\mu_0 \neq \mu_1\).

Optimal Sample Size: Equal Variances

Sample Size Formula

If \(\sigma_0 = \sigma_1 = \sigma\), the optimal sample size is:

\[N_0^* = N_1^* = N^* = 2(t_{\alpha/2} + t_\beta )^2(\frac{\sigma}{\delta})^2\]

Note: Just see that this formula is an inverse of calculating p-value.

Optimal Sample Size: Example

Sample Calculation

• Significance level \(\alpha\): 0.05.
• Power \(1-\beta\): 0.80.
• From standard normal tables: \(t_{\alpha/2} = 1.96\), \(t_\beta = 0.84\).
• To detect a half standard deviation change, you need 64 observations per treatment group. \[N^*= 2(1.96 + 0.84)^2 2^2 = 64\]

Optimal Sample Size: Key Considerations

Factors Affecting Sample Size

• Increases with the variance of outcomes.

• Non-linearly dependent on the significance level and power.

• Decreases with the square of the minimum detectable effect.

• Relative distribution of subjects across groups relates to outcome variances.

• Challenges in experimental economics: unknown effect size and variance, multiple hypothesis testing, and status quo bias.

Limitations to analytical power calculations

Limitations to analytical power calculations

• Only derived for some test statistics (differences of means)

• Makes specific assumptions about the data-generating process

• Incompatible with more complex designs

Simulation-based power calculation

Simulation-based power calculation

• Create dataset and simulate research design.

• Assumptions are necessary for simulation studies, but you make your own.

• For the DeclareDesign approach, see https://declaredesign.org/

Steps

• Define the sample and the potential outcomes function.

• Define the treatment assignment procedure.

• Create data.

• Assign treatment, then estimate the effect.

• Do this many times.

Examples

• Complete randomization

• With covariates

• With cluster randomization

Example: Simulation-based power for complete randomization

# install.packages("randomizr")


## Y0 is fixed in most field experiments.
## So we only generate it once:
make_Y0 <- function(N){  rnorm(n = N) }
repeat_experiment_and_test <- function(N, Y0, tau){
    Y1 <- Y0 + tau
    Z <- complete_ra(N = N)
    Yobs <- Z * Y1 + (1 - Z) * Y0
    estimator <- lm_robust(Yobs ~ Z)
    pval <- estimator$p.value[2]
    return(pval)
}

Example: Simulation-based power for complete randomization

power_sim <- function(N,tau,sims){
    Y0 <- make_Y0(N)
    pvals <- replicate(n=sims,
      repeat_experiment_and_test(N=N,Y0=Y0,tau=tau))
    pow <- sum(pvals < .05) / sims
    return(pow)
}

set.seed(12345)
power_sim(N=80,tau=.25,sims=100)

[1] 0.15

power_sim(N=80,tau=.25,sims=100)

[1] 0.21

Example: Using DeclareDesign

P0 <- declare_population(N,u0=rnorm(N))
# declare Y(Z=1) and Y(Z=0)
O0 <- declare_potential_outcomes(Y_Z_0 = 5 + u0, Y_Z_1 = Y_Z_0 + tau)
# design is to assign m units to treatment
A0 <- declare_assignment(Z=conduct_ra(N=N, m=round(N/2)))
# estimand is the average difference between Y(Z=1) and Y(Z=0)
estimand_ate <- declare_inquiry(ATE=mean(Y_Z_1 - Y_Z_0))
R0 <- declare_reveal(Y,Z)
design0_base <- P0 + A0 + O0 + R0

## For example:
design0_N100_tau25 <- redesign(design0_base,N=100,tau=.25)
dat0_N100_tau25 <- draw_data(design0_N100_tau25)
head(dat0_N100_tau25)

   ID         u0 Z    Y_Z_0    Y_Z_1        Y
1 001 -0.2060421 0 4.793958 5.043958 4.793958
2 002 -0.5874759 0 4.412524 4.662524 4.412524
3 003 -0.2908008 1 4.709199 4.959199 4.959199
4 004 -2.5648996 0 2.435100 2.685100 2.435100
5 005 -1.8967213 0 3.103279 3.353279 3.103279
6 006 -1.6400715 1 3.359928 3.609928 3.609928

with(dat0_N100_tau25,mean(Y_Z_1 - Y_Z_0)) # true ATE

[1] 0.25

with(dat0_N100_tau25,mean(Y[Z==1]) - mean(Y[Z==0])) # estimate

[1] 0.5569162

Example: Using DeclareDesign

# Estimate the treatment effect using a t-test
lm_robust(Y~Z,data=dat0_N100_tau25)$coef # estimate

(Intercept)           Z 
  4.8457631   0.5569162 

E0 <- declare_estimator(Y~Z,model=lm_robust,label="t test 1",
                        inquiry="ATE")
t_test <- function(data) {
       test <- with(data, t.test(x = Y[Z == 1], y = Y[Z == 0]))
       data.frame(statistic = test$statistic, p.value = test$p.value)
}
T0 <- declare_test(handler=label_test(t_test),label="t test 2")
design0_plus_tests <- design0_base + E0 + T0

design0_N100_tau25_plus <- redesign(design0_plus_tests,N=100,tau=.25)

## Only repeat the random assignment, not the creation of Y0. Ignore warning
names(design0_N100_tau25_plus)

[1] "P0"       "A0"       "O0"       "R0"       "t test 1" "t test 2"

design0_N100_tau25_sims <- simulate_design(design0_N100_tau25_plus,
          sims=c(1,100,1,1,1,1)) # only repeat the random assignment
# design0_N100_tau25_sims has 200 rows (2 tests * 100 random assignments)
# just look at the first 6 rows
head(design0_N100_tau25_sims)

                   design   N  tau sim_ID estimator term  estimate std.error
1 design0_N100_tau25_plus 100 0.25      1  t test 1    Z 0.1107677 0.2149666
2 design0_N100_tau25_plus 100 0.25      1  t test 2 <NA>        NA        NA
3 design0_N100_tau25_plus 100 0.25      2  t test 1    Z 0.2458211 0.2154258
4 design0_N100_tau25_plus 100 0.25      2  t test 2 <NA>        NA        NA
5 design0_N100_tau25_plus 100 0.25      3  t test 1    Z 0.5463041 0.2133367
6 design0_N100_tau25_plus 100 0.25      3  t test 2 <NA>        NA        NA
  statistic   p.value   conf.low conf.high df outcome inquiry step_1_draw
1 0.5152789 0.6075185 -0.3158265 0.5373619 98       Y     ATE           1
2 0.5152789 0.6075435         NA        NA NA    <NA>    <NA>           1
3 1.1410944 0.2566114 -0.1816843 0.6733266 98       Y     ATE           1
4 1.1410944 0.2566230         NA        NA NA    <NA>    <NA>           1
5 2.5607596 0.0119701  0.1229443 0.9696640 98       Y     ATE           1
6 2.5607596 0.0120273         NA        NA NA    <NA>    <NA>           1
  step_2_draw
1           1
2           1
3           2
4           2
5           3
6           3

Example: Using DeclareDesign

Now count the number of simulations where the p-value is less than 0.05.

# A tibble: 2 × 2
  estimator   pow
  <chr>     <dbl>
1 t test 1    0.2
2 t test 2    0.2

Power with covariate adjustment

Covariate adjustment and power

• Covariate adjustment can improve power because it mops up variation in the outcome variable.

  • If prognostic, covariate adjustment can reduce variance dramatically. Lower variance means higher power.

  • If non-prognostic, power gains are minimal.

• All covariates must be pre-treatment. Do not drop observations on account of missingness.

  • See the module on threats to internal validity and the 10 things to know about covariate adjustment.

• Freedman’s bias as n of observations decreases and K covariates increases.

Blocking

• Blocking: randomly assign treatment within blocks

  • “Ex-ante” covariate adjustment

  • Higher precision/efficiency implies more power

  • Reduce “conditional bias”: association between treatment assignment and potential outcomes

  • Benefits of blocking over covariate adjustment clearest in small experiments

Example: Simulation-based power with a covariate

## Y0 is fixed in most field experiments. So we only generate it once
make_Y0_cov <- function(N){
    u0 <- rnorm(n = N)
    x <- rpois(n=N,lambda=2)
    Y0 <- .5 * sd(u0) * x + u0
    return(data.frame(Y0=Y0,x=x))
 }
##  X is moderarely predictive of Y0.
test_dat <- make_Y0_cov(100)
test_lm  <- lm_robust(Y0~x,data=test_dat)
summary(test_lm)

Call:
lm_robust(formula = Y0 ~ x, data = test_dat)

Standard error type:  HC2 

Coefficients:
            Estimate Std. Error t value  Pr(>|t|) CI Lower CI Upper DF
(Intercept)   0.1100    0.18801  0.5852 5.598e-01  -0.2631   0.4831 98
x             0.4404    0.08137  5.4128 4.411e-07   0.2790   0.6019 98

Multiple R-squared:  0.231 ,    Adjusted R-squared:  0.2232 
F-statistic:  29.3 on 1 and 98 DF,  p-value: 4.411e-07

Example: Simulation-based power with a covariate

Example: Simulation-based power with a covariate

set.seed(12345)
power_sim_cov(N=80,tau=.25,sims=100)

[1] 0.13

power_sim_cov(N=80,tau=.25,sims=100)

[1] 0.19

Power for cluster randomization

Power and clustered designs

• Recall the randomization module.

• Given a fixed \(N\), a clustered design is weakly less powered than a non-clustered design.

  • The difference is often substantial.

• We have to estimate variance correctly:

  • Clustering standard errors (the usual)
  • Randomization inference

• To increase power:

  • Better to increase number of clusters than number of units per cluster.
  • How much clusters reduce power depends critically on the intra-cluster correlation (the ratio of variance within clusters to total variance).

A note on clustering in observational research

• Often overlooked, leading to (possibly) wildly understated uncertainty.

  • Frequentist inference based on ratio \(\hat{\beta}/\hat{se}\)

  • If we underestimate \(\hat{se}\), we are much more likely to reject \(H_0\). (Type-I error rate is too high.)

• Many observational designs much less powered than we think they are.

Example: Simulation-based power for cluster randomization

## Y0 is fixed in most field experiments. So we only generate it once
make_Y0_clus <- function(n_indivs,n_clus){
    # n_indivs is number of people per cluster
    # n_clus is number of clusters
    clus_id <- gl(n_clus,n_indivs)
    N <- n_clus * n_indivs
    u0 <- fabricatr::draw_normal_icc(N=N,clusters=clus_id,ICC=.1)
    Y0 <- u0
    return(data.frame(Y0=Y0,clus_id=clus_id))
 }

test_dat <- make_Y0_clus(n_indivs=10,n_clus=100)
# confirm that this produces data with 10 in each of 100 clusters
table(test_dat$clus_id)

  1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20 
 10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10 
 21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36  37  38  39  40 
 10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10 
 41  42  43  44  45  46  47  48  49  50  51  52  53  54  55  56  57  58  59  60 
 10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10 
 61  62  63  64  65  66  67  68  69  70  71  72  73  74  75  76  77  78  79  80 
 10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10 
 81  82  83  84  85  86  87  88  89  90  91  92  93  94  95  96  97  98  99 100 
 10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10  10 

Example: Simulation-based power for cluster randomization

[1] 0.09654799

Example: Simulation-based power for cluster randomization

power_sim_clus <- function(n_indivs,n_clus,tau,sims){
    dat <- make_Y0_clus(n_indivs,n_clus)
    N <- n_indivs * n_clus
    # randomize treatment sims times
    pvals <- replicate(n=sims,
                repeat_experiment_and_test_clus(N=N,tau=tau,
                                Y0=dat$Y0,clus_id=dat$clus_id))
    pow <- sum(pvals < .05) / sims
    return(pow)
}

Example: Simulation-based power for cluster randomization

set.seed(12345)
power_sim_clus(n_indivs=8,n_clus=100,tau=.25,sims=100)

[1] 0.66

power_sim_clus(n_indivs=8,n_clus=100,tau=.25,sims=100)

[1] 0.68

Example: Simulation-based power for cluster randomization (DeclareDesign)

P1 <- declare_population(N = n_clus * n_indivs,
    clusters=gl(n_clus,n_indivs),
    u0=draw_normal_icc(N=N,clusters=clusters,ICC=.2))
O1 <- declare_potential_outcomes(Y_Z_0 = 5 + u0, Y_Z_1 = Y_Z_0 + tau)
A1 <- declare_assignment(Z=conduct_ra(N=N, clusters=clusters))
estimand_ate <- declare_inquiry(ATE=mean(Y_Z_1 - Y_Z_0))
R1 <- declare_reveal(Y,Z)
design1_base <- P1 + A1 + O1 + R1 + estimand_ate

## For example:
design1_test <- redesign(design1_base,n_clus=10,n_indivs=100,tau=.25)
test_d1 <- draw_data(design1_test)
# confirm all individuals in a cluster have the same treatment assignment
with(test_d1,table(Z,clusters))

   clusters
Z     1   2   3   4   5   6   7   8   9  10
  0 100   0 100 100 100   0   0 100   0   0
  1   0 100   0   0   0 100 100   0 100 100

# three estimators, differ in se_type:
E1a <- declare_estimator(Y~Z,model=lm_robust,clusters=clusters,
                         se_type="CR2", label="CR2 cluster t test",
                         inquiry="ATE")
E1b <- declare_estimator(Y~Z,model=lm_robust,clusters=clusters,
                         se_type="CR0", label="CR0 cluster t test",
                         inquiry="ATE")
E1c <- declare_estimator(Y~Z,model=lm_robust,clusters=clusters,
                         se_type="stata", label="stata RCSE t test",
                         inquiry="ATE")

design1_plus <- design1_base + E1a + E1b + E1c

design1_plus_tosim <- redesign(design1_plus,n_clus=10,n_indivs=100,tau=.25)

Example: Simulation-based power for cluster randomization (DeclareDesign)

## Only repeat the random assignment, not the creation of Y0. Ignore warning
## We would want more simulations in practice.
set.seed(12355)
design1_sims <- simulate_design(design1_plus_tosim,
                    sims=c(1,1000,rep(1,length(design1_plus_tosim)-2)))
design1_sims %>% group_by(estimator) %>%
  summarize(pow=mean(p.value < .05),
    coverage = mean(estimand <= conf.high & estimand >= conf.low),
    .groups="drop")

# A tibble: 3 × 3
  estimator            pow coverage
  <chr>              <dbl>    <dbl>
1 CR0 cluster t test 0.155    0.911
2 CR2 cluster t test 0.105    0.936
3 stata RCSE t test  0.131    0.918

Example: Simulation-based power for cluster randomization (DeclareDesign)

## This may be simpler than the above:
d1 <- block_cluster_two_arm_designer(N_blocks = 1,
    N_clusters_in_block = 10,
    N_i_in_cluster = 100,
    sd_block = 0,
    sd_cluster = .3,
    ate = .25)
#d1_plus <- d1 + E1b + E1c
# d1_sims <- simulate_design(d1_plus,sims=c(1,1,1000,1,1,1,1,1))

Example: Simulation-based power for cluster randomization (DeclareDesign)

# d1_sims %>% group_by(estimator) %>% summarize(pow=mean(p.value < .05),
#    coverage = mean(estimand <= conf.high & estimand >= conf.low),
#    .groups="drop")

Comparative statics

Comparative Statics

• Power is:
  • Increasing in \(N\)
  • Increasing in \(|\tau|\)
  • Decreasing in \(\sigma\)

Power by sample size

some_ns <- seq(10,800,by=10)
pow_by_n <- sapply(some_ns, function(then){
    pwr.t.test(n = then, d = 0.25, sig.level = 0.05)$power
            })
plot(some_ns,pow_by_n,
    xlab="Sample Size",
    ylab="Power")
abline(h=.8)

## See https://cran.r-project.org/web/packages/pwr/vignettes/pwr-vignette.html
## for fancier plots
## ptest <-  pwr.t.test(n = NULL, d = 0.25, sig.level = 0.05, power = .8)
## plot(ptest)

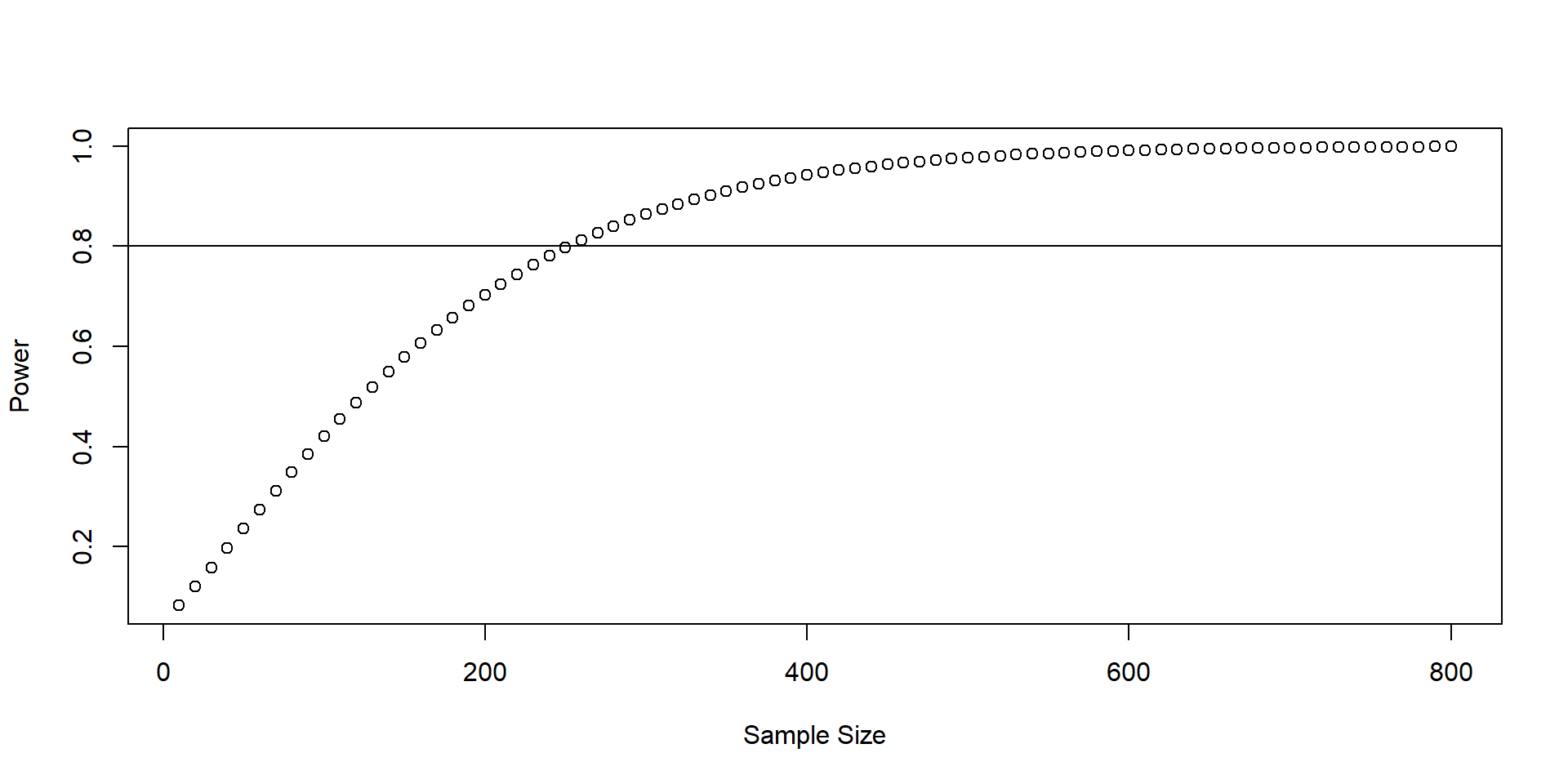
Power by treatment effect size

some_taus <- seq(0,1,by=.05)
pow_by_tau <- sapply(some_taus, function(thetau){
    pwr.t.test(n = 200, d = thetau, sig.level = 0.05)$power
            })
plot(some_taus,pow_by_tau,
    xlab="Average Treatment Effect (Standardized)",
    ylab="Power")
abline(h=.8)

Comments

• Know your outcome variable.

• What effects can you realistically expect from your treatment?

• What is the plausible range of variation of the outcome variable?

  • A design with limited possible movement in the outcome variable may not be well-powered.

Conclusion: How to improve your power

1. Increase the \(N\)

• If clustered, increase the number of clusters if at all possible

2. Strengthen the treatment

3. Improve precision

• Covariate adjustment

• Blocking

4. Better measurement of the outcome variable