ECON6037 Experimental Economics
Randomization
February 5, 2024
Randomization of treatment assignment
Randomization of treatment assignment
Randomization means that every observation has a known probability of assignment to experimental conditions between 0 and 1.
- No unit in the experimental sample is assigned to treatment with certainty (probability = 1) or to control with certainty (probability = 0).
Units can vary in their probability of treatment assignment.
For example, the probability might vary by group: women might have a 25% probability of being assigned to treatment while men have a different probability.
It can even vary across individuals, though that would complicate your analysis.
Random assignment vs. random sampling
Randomization (of treatment): assigning subjects with known probability to experimental conditions.
This random assignment of treatment can be combined with any kind of sample (random sample, convenience sample, etc.).
But the size and other characteristics of your sample will affect your power and your ability to extrapolate from your finding to other populations.
Random sampling (from population): selecting subjects into your sample from a population with known probability.
Randomization is powerful (1)
We want the ATE, \(\bar{\tau_i}= \overline{Y_i(1)-Y_i(0)}\).
We will make use of the fact that the average of differences equals the difference of averages:
ATE \(= \overline{Y_i(1)-Y_i(0)} = \overline{Y_i(1)}-\overline{Y_i(0)}\)
Randomization is powerful (2)
Let’s randomly assign some of our units to the treatment condition. For these treated units, we measure the outcome \(Y_i|T_i=1\), which is the same as \(Y_i(1)\) for these units.
Because these units were randomly assigned to treatment, these \(Y_i=Y_i(1)\) for the treated units represent the \(Y_i(1)\) for all our units.
In expectation (or on average across repeated experiments (written \(E_R[\cdot]\))):
\(E_R[\bar{Y_i}|T_i=1]=\overline{Y_i(1)}\).
\(\overline{Y}|T_i=1\) is an unbiased estimator of the population mean of potential outcomes under treatment.
The same logic applies for units randomly assigned to control:
\(E_R[\overline{Y_i}|T_i=0]=\overline{Y_i(0)}\).
Randomization is powerful (3)
- So we can write down an estimator for the ATE:
\(\hat{\overline{\tau_i}} = ( \overline{Y_i(1)} | T_i = 1 ) - ( \overline{Y_i(0)} | T_i = 0 )\)
- In expectation, or on average across repeated experiments, \(\hat{\overline{\tau_i}}\) equals the ATE:
\(E_R[Y_i| T_i = 1 ] - E_R[Y_i | T_i = 0] = \overline{Y_i(1)} - \overline{Y_i(0)}\).
- So we can just take the difference of these unbiased estimators of \(\overline{Y_i(1)}\) and \(\overline{Y_i(0)}\) to get an unbiased estimate of the ATE.
Random sampling
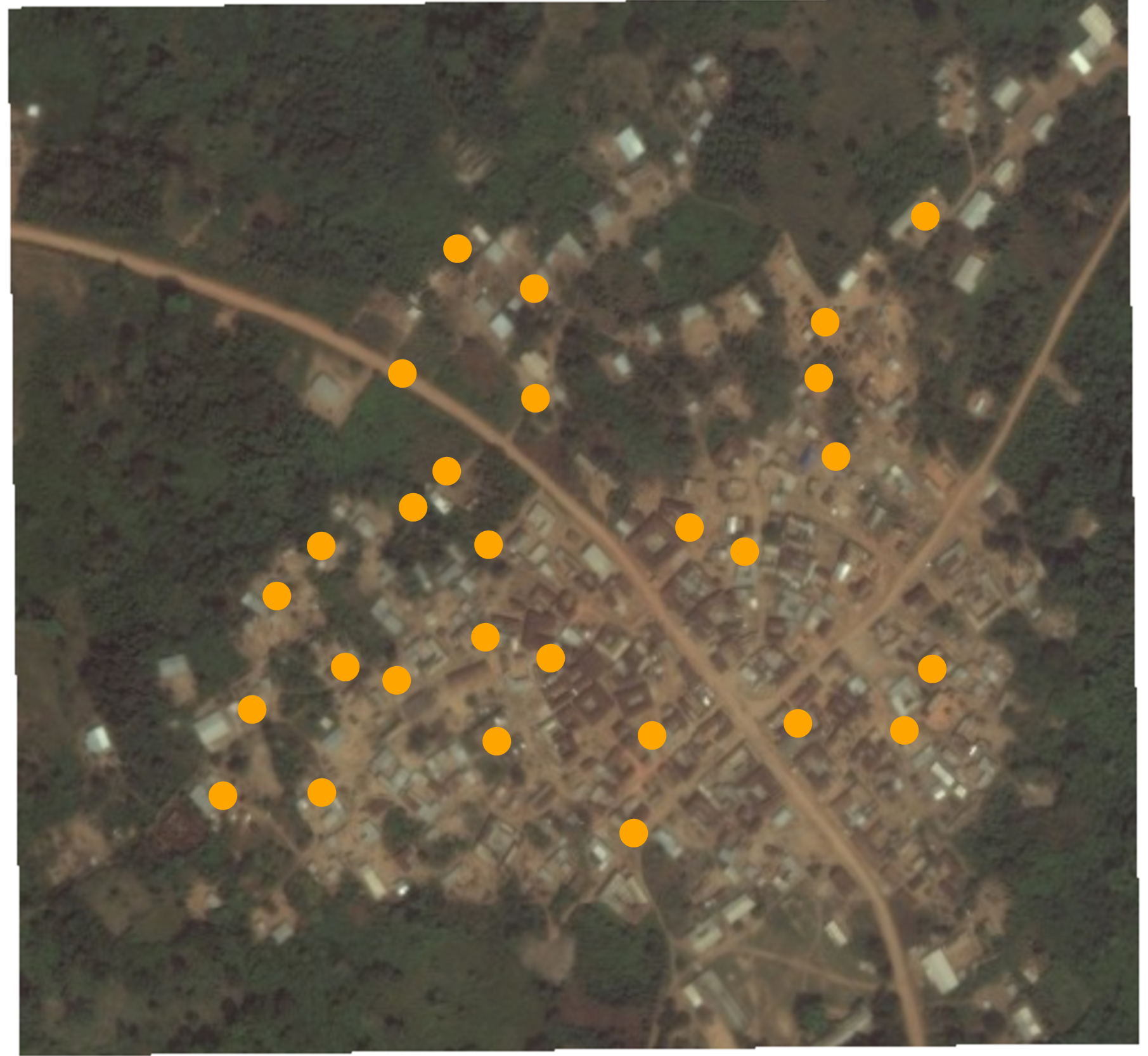
Random sample of households
Potential outcomes
Each household \(i\) has \(Y_i(1)\) and \(Y_i(0)\).

Random assignment to red (1) or blue (0) condition
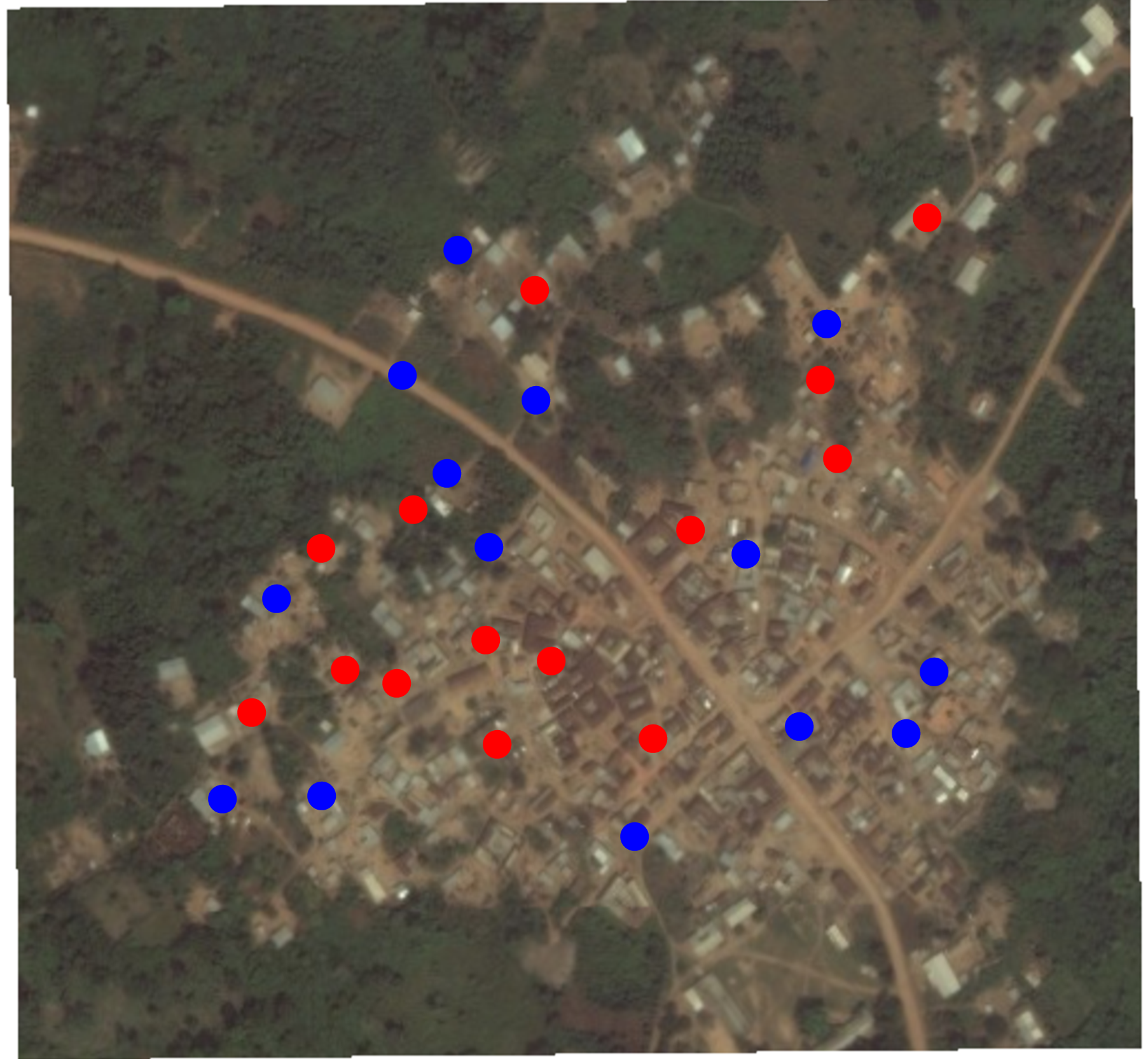
Random assignment of this random sample of households
Three key assumptions
To make causal claims with an experiment (or to judge whether we believe a study’s claims), we need three core assumptions:
Random assignment of subjects to treatment, which implies that receiving the treatment is statistically independent of subjects’ potential outcomes.
Stable unit treatment value assumption (SUTVA).
Excludability, which means that a subject’s potential outcomes respond only to the defined treatment, not other extraneous factors that may be correlated with treatment.
Key assumption: SUTVA, part 1
No interference – A subject’s potential outcome reflects only whether that subject receives the treatment himself/herself. It is not affected by how treatments happen to be allocated to other subjects.
A classic violation is the case of vaccines and their spillover effects.
Say I am in the control condition (no vaccine). If whether I get sick (\(Y_i(0)\)) depends on other people’s treatment status (whether they take the vaccine), it’s like I have two different \(Y_i(0)\)!
SUTVA (= stable unit treatment value assumption)
Key assumption: SUTVA, part 2
No hidden variations of the treatment
Say treatment is taking a vaccine, but there are two kinds of vaccines and they have different ingredients.
An example of a violation is when whether I get sick when I take the vaccine (\(Y_i(1)\)) depends on which vaccine I got. We would have two different \(Y_i(1)\)!
Key assumption: Excludability
Treatment assignment has no effect on outcomes except through its effect on whether treatment was received.
Important to define the treatment precisely.
Important to also maintain symmetry between treatment and control groups (e.g., through blinding, having the same data collection procedures for all study subjects, etc.), so that treatment assignment only affects the treatment received, not other things like interactions with researchers that you don’t want to define as part of the treatment.
Randomization is powerful (4)
If the intervention is randomized, then who receives or doesn’t receive the intervention is not related to the characteristics of the potential recipients.
Randomization makes those who were randomly selected to not receive the intervention to be good stand-ins for the counterfactuals for those who were randomly selected to receive the treatment, and vice versa.
We have to worry about this if the intervention were not randomized (= an observational study).
Randomized vs. observational studies
Different types of studies
Randomized studies
- Randomize treatment, then go measure outcomes
Observational studies
- Treatment is not randomly assigned. It is observed, but not manipulated.
Exercise: Learning about your prior knowledge
Discuss in small groups: Helpdesign the projects to answer one of these questions (or one of your own causal questions). Just sketch the key features of two designs — one observational and the other randomized.
Example research questions:
Do better housing conditions reduce domestic violence?
Can community monitoring increase clinic utilization and decrease child mortality in Uganda?
Exercise: Observational studies vs. Randomized studies
Tasks:
Sketch an ideal observational study design (no randomization, no researcher control but infinite resources for data collection). What questions would critical readers ask when you claim that your results reflect a causal relationship?
Sketch an ideal experimental study design (including randomization). What questions would critical readers ask when you claim that your results reflect a causal relationship?
Discuss
What were key components and strengths and weaknesses of the randomized studies?
What were key components and strengths and weaknesses of the observational studies?
Generalizability and external validity
Randomization brings high internal validity to a study – confidence that we have learned the causal effect of a treatment on an outcome.
But the finding from a particular study in one particular place and at one particular time may not hold in other settings (i.e., external validity).
This is a general concern, not just a concern for randomized studies.